Understanding excitation energies beyond the MO picture

Is it possible to get an intuitive understanding of electronic excitation energies that truly goes beyond the MO picture? This is what we are discussing in our newest preprint: Toward an Understanding of Electronic Excitation Energies Beyond the Molecular Orbital Picture. This is basically a sequel to my previous post HOMO-LUMO gaps and excitation energies, which seems to consistently attract visitors to this blog. In fact the paper started out as a short sequel and then it turned into 19 dense pages. Well, I hope it is worth the effort.

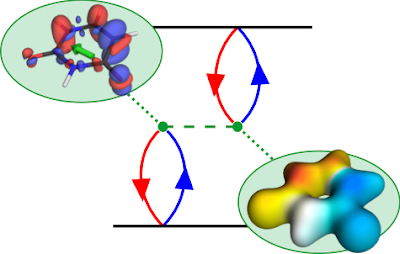
The TOC shows a diagrammatic representation of the exchange repulsion, which is responsible for the difference in energies between singlet and triplet states. The red and blue lines refer to the hole and electron, respectively. The dotted green line is the Coulomb interaction. The diagram is read in the following way: The hole and electron come together on the bra (bottom) and ket (top) side forming the transition density. They interact with each other via the Coulomb interaction. The resulting term can be interpreted as the Coulomb repulsion of the transition density with respect to itself. To represent this, we show the transition density and its electrostatic potential (ESP). The exchange repulsion is now simply an overlap between density and ESP.

The state shown is the first ππ* state of uracil. A closer look at the transition density (upper left) shows the expected π contributions. But why are there also σ contributions? It turns out that the pure ππ* state would have an excessively high exchange repulsion. That is why σ contributions are mixed in to lower the energy. These σ contributions lower the transition moment (shown in green) and, thus, have a direct experimentally observable consequence. They also mean that any description of the state in terms of only n and π orbitals is insufficient, which explains the problems of CASSCF in describing these sorts of states - called ionic states in the valence-bond description.