Ribonuclease A

Here is some stuff from my last lab [1]. The objective was to do force field calculations (with CHARMM) on our protein of choice. What I picked is Ribonuclease A, the enzyme that digests RNA in our food.

Ribonoclease A is a sturdy little molecule with 124 amino acids. Its four disulfide bridges (yellow in the picture) make it very stable and comparably easy to isolate. Just 124 amino acids also makes it nice for computations. The pictures were made with VMD which makes nice pictures and is also a pretty versatile tool that reads tons of file formats.


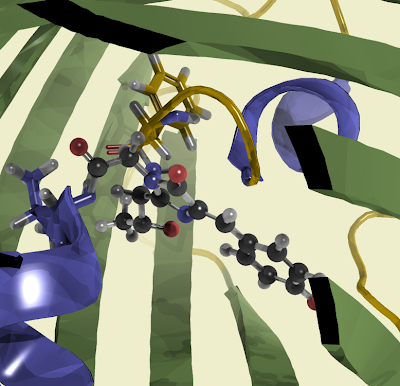
The active group of Ribonuclease A comes from two Histidine (black) residues that help hydrolizing the phosphate in the nucleic acid. Lysine (orange) provides the positive charge to interact with negatively charged phosphate groups.

The first thing you can do with a molecular structure is an energy minimization. These are the C_α traces of the crystal structure (yellow) and the vacuum optimized structure (red). They are in fact quite different even though the red structure is just the next local minimum.

The major problem with this optimization is that I did not include solvent effects. The electrostatic interaction energy (in the macroscopic limit) is given by

The crucial part is ε_r, the relative dielectric constant of the medium. In water ε_r=78. In other words: charges are strongly shielded compared to a vacuum. In the microscopic world things aren't as simple but it is still the same trend. The difference is probably a major reason why the structures are so different.

Another thing you can do with structures is normal mode analysis. That means computing the eigenvalues/eigenvectors of the mass weighted energy Hessian matrix which correspond to the frequencies/motions of the normal modes. Ribonuclease A is small for a protein but it still has 1856 atoms. So we have 3x1856=5568 degrees of freedom. We have to compute, store and process about 30 million matrix elements. This seems much but these days most regular computers will be able to do this in less than half an hour. 30 million matrix elements corresponds to something like 300 MByte, nothing too crazy. [2]

These are the three lowest frequency modes (aside from translation and rotation) of Ribonuclease A. They are large scale backbone motions. A weak force constant and a high effective mass causes them to have wave numbers below 10/cm.

---

[1] Not the kind of lab where you need a lab coat.

[2] Actually if you are just interested in a few eigenvalues and -vectors, you can go much higher. For example multi-reference configuration interaction with Columbus (which is a great program by the way....): finding the first 4 states out of a 8569890 x 8569890 matrix was possible within about 17 hours. In this case you don't store trillions (7E13) of matrix elements and do a diagonalization. You use the iterative Davidson procedure which will find an eigenvector close to a starting guess.

GFP pictures

Time for some more graphics. I picked GFP which is not really a new idea but it is a pretty cool molecule.

In the sphere model all proteins pretty much look alike. But I still think kind of cool, especially if you use Lightnir's QuteMol preset for pymol.
The cartoon model shows you more about the structure. GFP consists of a β-sheet "barrel" that encapsulates the chromophore. You need a rigid structure if you want to make sure that the chromophore does not quench before it is able to show fluorescence. It is interesting to compare this to Rhodopsin which is apparently much more flexible. This makes sense since in Rhodopsin the biological activity is related to non-radiative decay and isomerisation.

The chromophore is trapped at the center of the barrel.


Interestingly the chromophore is made directly out of amino acids. You can take a look at it and think of how this is done.

The answer is here. The hydroxyphenyl comes from tyrosine (as expected). The imidazolon ring is formed after cyclization, the bridging double bond through oxidation. It is interesting to consider that this apparently works in many different organisms and not just in the jelly fish aequoria victoria. The driving force seems to be that the amino acids are pressed together in the barrel.

The chromophore is part of the protein chain. It is connected to the helix that goes through the center of the protein.

Or from a different perspective.

QMC@home

What you need in computational chemistry is - not so very surprisingly - computers. You can either use your own little cluster. You can try to get time at a super computer. Or you can have other people do the work for you.

Actually I am advertising for the competition a little bit but I think the idea is pretty cool. You are probably used to distributed computing with the SETI project. QMC@home does the same in quantum chemistry. The disadvantage of their Quantum Monte Carlo approach is that you need a huge amount of computer time. The advantage is that you can easily distribute it over many computers with little communication between them. The ideal case for voluntary grid computing. It is organised over the same BOINC platform that is also used by the SETI project. So if you download it and get bored by Quantum Monte Carlo, you can switch the system and start looking for extra terrestrial life.

QMC@home has this screensaver that tells you what's going on. (In principle it should have it, it's not working on my computer).


In this case they are computing interaction energies for the cytosine dimer. Van-der-Waals dispersion interactions are a difficult problem because you need a highly correlated wave function to describe them correctly. Maybe QMC is a good way to do it.

I like the idea because it seems like a waste to have so many unused computers standing around everywhere. It has to be said though, that the computation uses up energy. But then when I look at people that don't even turn off their screens when they leave their computers, it does not seem like they would complain about a little bit of extra energy use.
It would probably be a good idea if they had some kind of reimbursement system. But on the other hand it is kind of fun as it is and you get a sense of accomplishment just for keeping your computer on for some time. And now I also have an excuse for not turning it off every time I leave my workplace.