Chemical shielding tensors

How do you visualise a tensor field? A 3x3 tensor as a function of the 3 spatial coordinates makes a 12-dimensonal object. How do we visualise a 12-dimensional object using a 2-dimensional screen? This is the problem we encountered trying to visualise the chemical shielding tensor, which is a common aromaticity criterion. The solution: we compute the principal axes of the tensor and represent those using little dumb-bells at different points in space providing us at least a coarse-grained description.

 To get the full story, check out our preprint “3D Visualisation of chemical shielding tensors to elucidate aromaticity and antiaromaticity” available on ChemRxiv or this blog post.

Here, I just wanted to show a few more computer graphics. This, for example, are the in-plane shielding tensors shown with our new VIST method in connection with the ACID isosurface as computed via GIMIC.

For comparison, the NICS(1) tensors along with the magnetically induced current densities also computed using GIMIC. Diatropic currents, giving rise to positive shielding are shown in blue; paratropic currents in red. Diatropic currents dominate, hence we see positive (blue) shielding.

The code will be released through TheoDORE once I have the time to make it reasonbly well documented and user friendly.

De-excitations

If the electronic ground state of a molecule has double-excitation character and the excited state only single-excitation character, then you can view the molecule as being "de-excited." Electrons are taken from a higher lying orbital and moved into a lower lying orbital. A recent paper tries to formalise this idea by computing an expectation value of the particle-hole permutation operator. We take the two-body exciton wavefunction, switch the electron and hole and see how much it resembles the original wavefunction. If the hole resides purely in the occupied orbitals and the electron purely in the virtual orbitals, this has to yield zero. But with a correlated ground state it does not vanish.

The striking thing is that this expectation value of the particle-hole permutation operator seems to agree between TDDFT and wavefunction based methods in, both, magnitude and sign. This means that de-excitations are a "real thing" rather than just an artifact of TDDFT - not physically observable but a well-defined property of the wavefunction. For more on this, see PCCP 2020, 22, 6058.

Understanding excitation energies beyond the MO picture

Is it possible to get an intuitive understanding of electronic excitation energies that truly goes beyond the MO picture? This is what we are discussing in our newest preprint: Toward an Understanding of Electronic Excitation Energies Beyond the Molecular Orbital Picture. This is basically a sequel to my previous post HOMO-LUMO gaps and excitation energies, which seems to consistently attract visitors to this blog. In fact the paper started out as a short sequel and then it turned into 19 dense pages. Well, I hope it is worth the effort.

The TOC shows a diagrammatic representation of the exchange repulsion, which is responsible for the difference in energies between singlet and triplet states. The red and blue lines refer to the hole and electron, respectively. The dotted green line is the Coulomb interaction. The diagram is read in the following way: The hole and electron come together on the bra (bottom) and ket (top) side forming the transition density. They interact with each other via the Coulomb interaction. The resulting term can be interpreted as the Coulomb repulsion of the transition density with respect to itself. To represent this, we show the transition density and its electrostatic potential (ESP). The exchange repulsion is now simply an overlap between density and ESP.

The state shown is the first ππ* state of uracil. A closer look at the transition density (upper left) shows the expected π contributions. But why are there also σ contributions? It turns out that the pure ππ* state would have an excessively high exchange repulsion. That is why σ contributions are mixed in to lower the energy. These σ contributions lower the transition moment (shown in green) and, thus, have a direct experimentally observable consequence. They also mean that any description of the state in terms of only n and π orbitals is insufficient, which explains the problems of CASSCF in describing these sorts of states - called ionic states in the valence-bond description.

Visualising electron correlation

How do you visualise the correlation between two particles? One option is to fix one of them at a specific region of space and look at the distribution of the other one. This is the principle behind a new method for visualising excitonic correlation just presented in a paper in ChemPhotoChem: Visualisation of Electronic Excited‐State Correlation in Real Space, and released within the TheoDORE 2.0 code. First, we have to interpret the excited state within the electron-hole picture as explained previously and compute the two-body electron-hole distribution. Then, we can fix one of the quasi-particles in space and observe the distribution of the other one.

Below, I am showing what this analysis looks like for a simple PPV oligomer. I am fixing the hole either at the terminal phenyl, the vinyl or the central phenyl and plot the corresponding electron distribution. In the case of the S₁ state, the electron does not really care about the hole. The electron comfortably rests in the LUMO no matter what the hole does:

But for the S₂ state things look completely differently. The electron now tries to actively avoid the hole as it moves through the system.

S₃, for comparison, has a much more localised structure where the electron is always focussed on the centre.

S₄ has a somewhat more complicated structure:

By the way, I realised that the same type of analysis has been recently performed for periodic computations as well. The difference is that in a periodic system every atom (or symmetry unit) will produce the same picture. In a finite system the picture also changes with the position of the probe.

Electron donating and withdrawing groups

Aside from the fact that I do not believe in the existence of HOMOs and LUMOs, it is sometimes good to know how they work. In particular, I can never remember how electron-donating and withdrawing groups work. Here is how I understand it:

• An electron-donating group adds more electrons to the system and thus increases electron-electron repulsion (or decreases the effective nuclear charge). As a consequence the HOMO and LUMO energies increase.
• An electron-withdrawing group removes electrons and, thus decreases the HOMO and LUMO energies.
• An electron-donating group usually acts through an occupied non-bonding orbital. This is energetically close to the HOMO. Therefore, it has a stronger effect on the HOMO than on the LUMO (at least in organic molecules).
• An electron-withdrawing group acts through a virtual orbital, which interacts more strongly with the LUMO.
• As a consequence, electron-donating and withdrawing groups are both expected to lower the HOMO-LUMO gap in organic molecules.
• Things are different for transition metal complexes. For example an electron-withdrawing fluorine group still lowers orbital energies. But it can affect the HOMO more strongly and increase the overall gap in fluorinated iridium complexes, see this Ref.

Not all basis sets are created equal

Basis sets are not the most inspiring topic but you can't get around them. That is why we looked at them in our new paper. I am not discussing how many ζ you need or how many diffuse and polarization functions  but I am asking a more subtle question: how big are the differences between basis sets of the same formal type?

This question is addressed in our new paper "Detailed Wave Function Analysis for Multireference Methods: Implementation in the Molcas Program Package and Applications to Tetracene" [full text] that appeared in JCTC. The initial purpose of this paper was to introduce a new toolbox for analyzing multireference computations in the open-source OpenMolcas program package, and I want to encourage people to use this code.

But there is also an important take home message: basis sets of the same formal type (in this case polarized double-ζ) can perform vastly different. And this is not only reflected in the energies but also seen in the densities and overall wavefunctions. In the present case, an atomic natural orbital type basis set had a particularly good performance. This good performance comes at the cost of more primitive basis functions. But these primitive basis functions only play a role in the initial AO integral computations and do not affect the cost of the actual CASSCF/CASPT2 computation at all.

Local electron correlation

If you are interested in multireference methods that can be applied to large systems, then you can check out a new paper by us: "Local Electron Correlation Treatment in Extended Multireference Calculations: Effect of Acceptor-Donor Substituents on the Biradical Character of the Polyaromatic Hydrocarbon Heptazethrene" in JCTC. The paper reports a locally correlated implementation for the multireference configuration interaction method. The code is available within the COLUMBUS program package.
 

TDDFT for large conjugated systems

About five years ago, when we tried applying TDDFT to large conjugated systems, we noticed that it just did not work. This confused me for a while: What is so difficult about conjugated systems? Then I searched the literature, which showed that other people noticed the same problem quite a while ago (e.g. S. Grimme), that the phenomenon was interpreted in terms of exciton sizes, and that it was seen as "charge transfer in disguise." The thing that was still missing was a tangible way to analyze and talk about this problem. Therefore, we wanted to look at it from a somewhat different viewpoint. We took a set of conjugated polymers of varying sizes, performed TDDFT computations with different functionals, and analyzed the computations with our wavefunction analysis toolbox for TDDFT. The results are shown in our paper "Universal Exciton Size in Organic Polymers is Determined by Nonlocal Orbital Exchange in Time-Dependent Density Functional Theory" in JPCL.

The main quantity we are interested in is the exciton size, which corresponds to a dynamic charge transfer distance. The first striking observation is that the exciton size is largely independent of the molecular details but scales uniformly with the system size, as initially pointed out by Knupfer et al. The second point, important from a methodological point of view, is that huge variations between the functionals are observed. A bound exciton can only be formed if non-local exchange is included in the functional. The more non-local exchange is included, the stronger the observed binding.

Comparing Wavefunctions by their Overlap

Ever since starting in quantum chemistry I have been trying to avoid looking at orbitals. One reason is laziness. I just do not like sitting there clicking and waiting for all the orbitals to be rendered (even though this can be improved by using the proper scripts and programs). The other reason is a formal one: Orbitals, being one-body functions, can never tell us the whole truth about the many-body wavefunctions. Even worse, the same wavefunction may appear differently depending on the orbital set used to describe it (canonical orbitals, natural orbitals, natural transition orbitals, ...)

Assume that we performed two computations with different computational methods. When we look at the results we find out that, both, the molecular orbitals and wavefunction listings changed between the calculations. Does this mean that the two computations produced different wavefunctions? Not necessarily! The changes in the orbitals might be compensated by changes in the wavefunction expansion, at least in part. If we want to compare such wavefunctions we have to take into account the changes in the MOs and wavefunctions in a consistent fashion. In our newest Communication in J. Chem. Phys. "Unambiguous comparison of many-electron wavefunctions through their overlaps" we suggest to use the many-body wavefunction overlap for this task, i.e. the scalar product in the full many-body Hilbert space.

The outcome looks like this:

What we are doing is computing the 4 lowest excited states with CASSCF(12,9) and with MR-CIS(12,12). And then we compute the overlaps for all pairs of states and summarize them in pie charts. Every chart corresponds to one CASSCF wavefunction and the colors correspond to the MR-CIS wavefunctions. For example the second chart tells us that the Ψ₁' wavefunction at CASSCF has a 67% overlap with the Ψ₁ wavefunction at MR-CIS. But there are also smaller contributions of the Ψ₂ and Ψ₃ wavefunctions (as seen by the green and yellow bits).

The analysis gives us a quick overview of the relations between the wavefunctions computed at the different levels. There are two immediate conclusions: First, the overall state ordering is the same for both methods. Second, the wavefunctions are generally quite different, as seen by the large chunks of the pies missing.

The overlap code described here is actually a side product of a development we did for the nonadiabatic dynamics program SHARC (see this post). It will be released from the SHARC homepage as a standalone module, I hope soon ...

Entanglement Entropy of Electronic Excitations

There is more to excited states than meets the eye. Just looking at the orbitals will not tell you everything there is to know about the many-body wavefunctions. The purpose of my newest paper "Entanglement Entropy of Electronic Excitations," that just appeared in J. Chem. Phys., was to quantify the amount of information that is hidden from view. For this purpse, I used the idea of mutual information from quantum information theory.

The focus of this paper is the eigenvalue spectrum of the natural transition orbital (NTO) decomposition. There is information in the eigenvalue spectrum independent of the orbitals themselves. To illustrate the point, we can look at the first excited singlet state of two interacting ethylene molecules at 6.0 Å

and at 3.5 Å

The orbitals in both cases look similar but the eigenvalues λ₁ and λ₂ are different. For the larger separation both are equal at about 0.45. For the smaller separation, there is one dominant one at 0.86. Clearly, these are different wavefunctions, but what is the significance?

In the paper I am arguing that only the first case is consistent with the idea of a Frenkel exciton, i.e. two coupled local excitations. The second case can be seen as one homogeneous transition. This automatically means that there is admixture of charge transfer, since the orbitals are distributed evenly. And indeed when we apply our charge transfer measures, we find charge resonance character in the second case.

The whole formalism employed is somewhat abstract, unfortunately, and too much for one single blogpost. But the take home message is the following: Quantum and correlation effects appear even for rather simple excited state calculations. In critical cases these may mislead us when interpreting the calculations. Luckily, there is a solution to this conundrum - our wavefunction analysis tools TheoDORE and libwfa :)

More Conjugated Polymers

It looks like the exciton models we developed over the last years are actually reaching a level where "applied" people are becoming interested in them. I was very happy to have a joint project with S. Kraner from Dresden who wanted to examine universal properties of excitons in conjugated organic polymers. This collaboration lead to a new paper "Exciton size and binding energy limitations in one-dimensional organic materials" that just appeared in JCP.

The results showed that there is a quite universal relationship between molecular size and exciton size. The important point is, however, that the exciton size does not grow indefinitly with the molecular size. If the size of the π-system reaches about 40 Ang, no further enhancement of the exciton size occurs and a bound exciton remains.

Another point (and a reason why we had the pleasure to revise the manuscript quite a few times) is the fact that the results are strongly dependent on the exchange correlation functional. While the general trend of an exciton size limitation is present whenever you have some amount of Hartree-Fock exchange in the functional, the precise value differs, as discussed also in another recent paper by us. The reason is a correlation effect and ensuing dynamic charge transfer.

Conjugated Polymers

If you compute excited states in conjugated polymers, all you see is orbitals. Lots of orbitals, π and π* orbitals. So how do you describe the excited states? Are they all just ππ* states? Well, not really ... but the interesting part lies in correlation effects and quantum superpositions, things you don't see from the orbitals directly.

A while back I had the chance to play around with my wavefunction analysis tools on the polypara-phenylene-vinylene molecule in a first paper. It was fun, but it did not really satisfy me. That's why I convinced Steffi, a student in our group, to do a follow-up. Now, two years later, we finally submitted the material to PCCP where it can be found as our new article: "Excitons in poly(para phenylene vinylene): A quantum-chemical perspective based on high-level ab initio calculations".

The part, which I find most appealing is shown below. The figure shows the electron-hole correlation plots for the singlet excited states of the (PV)₇P oligomer. Here, the hole position is plotted along the x-axis and the electron position along the y-axis and the probability that the electron and hole reside at a specified position is coded in grey scale. Points along the main diagonal (going from lower left to upper right) are local excitations while off-diagonal contributions code for charge transfer. In these plots one can discern two types of features. Nodal planes perpendicular to the main diagonal indicate higher translational quasi-momentum, and nodal planes along the main diagonal correspond to different hydrogenic states of the exciton. The interesting thing is that the quasi-particle picture emerges directly from standard quantum chemical calculations. All you have to do, is look.

Correlation and Charge Transfer in TDDFT

The charge transfer problem of time-dependent density functional theory (TDDFT) is well known. TDDFT also has a problem for extended π-systems even if there is no net charge transfer. Is there a connection? Yes, correlation!

In a recent communication in J. Chem. Phys., Exciton analysis in time-dependent density functional theory: How functionals shape excited-state characters,  we discuss the relation between static and dynamic charge transfer effects and their description in TDDFT. It is shown that both kinds of charge transfer are detrimental to local functionals while the problems can be remedied through Hartree-Fock exchange. The results are interpreted in terms of excitonic correlation. Only the inclusion of Hartree-Fock exchange leads to bound excitons while effective electron-hole repulsion is obtained for local functionals.

Correlation

Electron correlation has always been this intangible thing to me. You can talk about correlation energy, about multi-configurational wavefunctions, about differences between dynamic and static correlation. But what is actually going on? Let's tackle the problem with statistics! This is what we did in our new paper Statistical analysis of electronic excitation processes: Spatial location, compactness, charge transfer, and electron-hole correlation in J. Comp. Chem.

How do you quantify correlation? With a correlation coefficient! All you need is a function in two variables, then you can compute its covariance and normalize it by the standard deviations. A logical choice for such a function would be the 2-body density and given enough time and/or people doing it for me, I will look at that. For now we chose the 1-particle transition density matrix (1TDM) between the ground and excited state. This function describes the electron and hole quasi-particles in the exciton picture (see this post). And, among other things, we can compute the correlation coefficient between the electron and hole.

A good way to understand this new tool is in the case of symmetric dimers. Because of the symmetry all orbitals and states in such a system are delocalized over the whole system and no net charge transfer can be seen. But it is clear that the charge transfer states do not disappear: They are just arranged in symmetric linear combinations yielding the charge resonance states. On the other hand the local excitations are arranged in excitonic resonance states. Applying the new tool to this type of system shows that the difference is a correlation effect: Positive correlation yields bound excitonic states while negative correlation represents charge resonance

Twisted Intramolecular Charge Transfer

Admittedly, we are not the only people working on Dimethylaminobenzonitrile (DMABN) and its dual fluoresence. But it is an interesting system worth looking at. Our paper about this topic "Intramolecular Charge Transfer Excited State Processes in 4-(N,N-Dimethylamino)benzonitrile: The Role of Twisting and the πσ* State" is finally released after starting this project about four years ago. Check it out if you are interested.

Löwdin orthogonalization

Did you know that you can do a Löwdin orthogonalization by a singular value decomposition? Usually, when I hear Löwdin orthogonalization, I think of some weird S^1/2 matrix, which scares me and I tend to stay away from it... But this pdf from the University of Oregon claims that you can do it in a different way. And it seems to work.

Say you have a matrix A and you want an orthogonal matrix that resembles it as closely as possible. What do you do? First you do a singular value decomposition of A:

Here U and V are orthogonal matrices and Λ is a diagonal matrix. We can now construct

which is an orthogonal matrix, since U and V are both orthogonal matrices. But even more, A' is the orthogonal matrix that best resembles A in the sense that for all orthogonal matrices Q it minimizes the distance with respect to the Frobenius norm

That is all you have to do.

Iridium complexes and the failure of ADC(2) to describe them

When I started working on iridium complexes two and a half years ago, there was one simple thing I could not explain: The results at the ADC(2) level were more than one eV off from the ADC(3) reference. And that is not good: you would not expect that a correlated ab-initio method would fail so badly. What followed was a two year detour through the world of excited state analysis (seen in some previous posts: [1], [2], [3], [4], [5]). And finally, I feel like I am in a position to discuss the above question properly in our new paper "High-Level Ab Initio Computations of the Absorption Spectra of Organic Iridium Complexes", which just appeared in JPCA.

The first step was to properly quantify the charge transferred using population analysis schemes. This revealed that ADC(2) had a strong bias toward overstabilizing charge transfer states. Usually you would think that this is a problem of TDDFT. But interestingly even TDDFT/B3LYP performed much better with errors only on the order of 0.5 eV.

To quantify the problem of ADC(2) we needed a new tool. For this purpose we took a closer look at the attachment/detachment analysis of Head-Gordon. While it is common to visualize the attachment and detachment densities, there is also an important meaning to the integral over them, the promotion number p. This quantity counts the total number of rearranged electrons and proved as a useful measure for orbital relaxation effects, which are difficult to understand otherwise.

So what happened when we made this analysis? At the ADC(1) level (whose energies and state densities are identical to CIS) p has to be equal to 1 per construction. Then ADC(2) apparently overestimates orbital relaxation effects with p values above 1.5. And only the ADC(3) level is balanced enough to cover some but not too much orbital relaxation.

HOMO-LUMO gaps and spin eigenfunctions

Statistically speaking, writing sequels is not a good idea,[1] but there is something I withheld from you in my previous post about HOMO-LUMO gaps and excitation energies: the spin of the electron. Spin makes everything a bit more complicated but also more interesting. What are the excitation energies of the singlet and triplet eigenfunctions? And what is exchange splitting?

Compared to last time, we have to construct spin-adapted eigenfunctions. Slater determinants  (constructed from restricted orbitals) are always eigenfunctions of S_z but not necessarily of S². One simple possibility of creating an S² eigenfunction is the construction of a high-spin determinant. And this is how I will start here. For example, we can create a spin-eigenfunction by exciting from spin-down occupied orbital k into the spin-up unoccopied orbital a. As shown in the previous post, the energy of the resulting determinant is given according to (here the bar marks the spin-down quantities)

The second (exchange type) integral vanishes and the expression can be rewritten as

In other words: In the triplet case the Coulomb interaction between electron and hole is the only relevant term.

If we are interested in the singlet then we have to consider linear combinations of excited determinants. The standard construction uses the spin-up and spin-down excited determinants

Here "plus" yields the singlet and "minus" the triplet. The energy of this wavefunction is expanded as:

The first two terms are the energies of the individual Slater determinants (as discussed in the last post). The third term is the coupling element, which is also readily calculated.

The spin-up and spin-down energies are equivalent and of the coupling terms only the first (exchange-like) one remains:

If we use the energy expression of the excited Slater determinant from the previous post we obtain for the singlet energy

When compared to the simple band picture, the energy is lowered by the Coulomb interaction between the electron and hole and raised by twice the exchange interaction. For the triplet we obtain

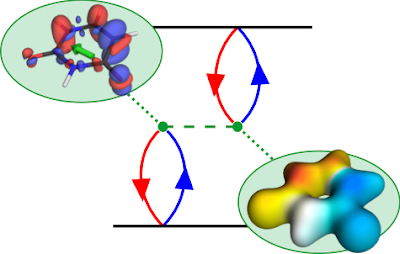
which is (luckily for me trying to write this down) the same as the high-spin triplet discussed above. There is only a Coulomb but no exchange interaction. The splitting between the singlet and triplet amounts to twice the exchange integral, hence it is called "exchange splitting".

The Coulomb term corresponds to the attraction between the hole density (computed as the square of orbital k) and the electron density (the square of orbital a). It is a long range interaction decaying with the reciprocal distance of the two orbitals. The exchange term is computed by multiplying orbitals k and a with each other (yielding the transition density) and computing the electrostatic repulsion of this with itself. It is a short range interaction, which requires that a and k occupy the same space. These considerations show that the triplet state will always be lesser or equal in energy than the corresponding triplet singlet state and that this is particularly pronounced for localized states.

---

[1] The problem is that there is a very low chance that the sequel to your best post will be your new very best post. Even if it is a good post, it will look bad in comparison to the original one. But this is only a question of the reference point and part of a general phenomenon called Regression to the Mean.

Multireference spin-orbit configuration interaction - perturbational treatment

If you are interested in multireference methods and/or relativistic effects, here is a new paper for you: "Perturbational treatment of spin-orbit coupling for generally applicable high-level multi-reference methods" in J. Chem. Phys. What we did is taking the existing spin-orbit CI code in Columbus and extended it for quasi-degenerate perturbation theory, which is in fact just a fancy way of saying that we stop the MR-CI after the first iteration (using the non-relativistic solutions as initial guesses). Besides that we needed an interface translating the CI vectors between the non-relativistic and relativistic representations.

With this tool we could compare the perturbational treatment with the full SO-CI. The agreement of the relative energies was quite good. But there was a significant difference in the total energies, since spin polarization was missing in the perturbational model space. But this was a systematic error affecting all states more or less the same.

The main reason why we wanted the perturbational approach is that it allows for the computation of gradients and non-adiabatic interactions (assuming that the spin-orbit couplings are slowly varying). And then we can do non-adiabatic dynamics with it. So far the methodology is implemented in SHARC with an application in this paper.

And finally, since they always look cool, a representation of the Shavitt graph coding the SO-CI configurations:

Orbital relaxation - the natural difference orbitals

As another example for the wavefunction analysis tools from last post, let us look at dimethylaminobenzonitrile (DMABN), a prototype charge transfer molecule and analyze the S₂ state. I will start with the natural transition orbitals (NTOs), the singular vectors of the transition density matrix. The S₂ state of DMABN has only one pair of NTOs with any significant contribution. To the left the hole, to the right the particle NTO are shown. In this representation the state can be clearly identified as a ππ* state with some partial charge transfer character (going from the amino to the nitrile side).

The hole and particle densities, i.e. the weighted sums over all NTOs, closely resemble these primary NTOs:

For comparison, we can look at the attachment/detachment densities as computed from the difference density matrix:

These look notably different from the hole and particle densities! What you can see at first sight, is that they are "bigger" - there is more happening. While the hole and particle densities contain 0.84 electrons each, the integral over the attachment and detachment densities is 1.41 e. To get a more detailed look at this, we can analyze the natural difference orbitals (NDOs), the eigenvectors of the difference density. Here for example the first three detachment and attachment NDOs and their respective eigenvalues:

-0.911	0.908
-0.060	0.059
-0.043	0.043

The first pair of NDOs corresponds to the NTOs as shown above. But aside from that, there are a number of additional contributions. The two most important ones are apparently polarizations of the σ-bonds: while the primary excitation process takes electrons from the π orbital at the amino N-atom, some of the electron density is restored through the σ-system. We can quantify this through a Mulliken analysis and find out that during the primary transition, the N-atom loses 0.33 e and gains 0.04, i.e. there is a primary charge shift of 0.29 e. By contrast the difference density tells us that 0.39 electrons are detached from N-atom and 0.19 are attached leading to a net charge shift of only 0.19 e on this atom. By construction the latter corresponds to the actual change in the Mulliken population. But, I guess also the former has a physical significance.

Anyway, I do not want to go into much more detail now. But I hope I could convince you that there is really a lot of exciting stuff happening with excited states (as the name suggests ...). And just looking at HOMOs and LUMOs is not going to help you with any of that. If you are interested, you can check out the two new papers (Part I, Part II), download the Wave Function Analysis Tools from my homepage, or use Columbus where some of these things are implemented as well. Unfortunately, the whole functionality is not released yet. But it will be made available soon within the ADC module of Q-Chem and as a separate C++ library. Let me know if you have any questions or any suggestions for applications.