This interpretation explains for example the linear relationship of the oscillator strength of the lowest excited state with system size in the case of some conjugated organic polymers (see e.g. this paper): If there are more electrons available to oscillate, then the transition strength increases.
The oscillator strength fij between two non-degenerate states i and j is defined (in atomic units) as two thirds of the squared transition dipole moment multiplied by the energy gap
where the vector r contains all 3N spatial coordinates of the N electronsThe Thomas-Reiche-Kuhn sum rule now states that the sum over the oscillator strengths from one state i to all possible other states is equal to the number of electrons in the system, i.e.
In particular, if we consider excitations from the ground state, then all oscillator strengths are positive. Which means that the oscillator strengths can in fact be viewed as a partitioning of the number of electrons.
The derivation of this sum rule starts by realizing that the momentum operator with respect to any spatial coordinate x of any particle (e.g. x=y2) is given as the commutator of the Hamiltonian with this coordinate
This follows whenever H is of the form
where clearly the derivatives with respect to x are the only part, which does not commute with x itself
By applying the product rule twice, the first term of this expression becomes
And in summary
The remaining proof follows what is shown here (sorry that I am switching the notation, but I copy-and-pasted a little bit ...). First one realizes that the commutator of x and px is equal to i
Then one expands the commutators and inserts a resolution of the identity over the eigenstates of the Hamiltonian
Insert the above expression for px
The commutators are evaluated by letting H act either on the bra or the ket, which results in a multiplication with the respective eigenvalue. And after summing together the equivalent terms one obtains
The actual r vector was composed of 3N individual electron coordinates. The above equation holds for each of these coordinates. Thus, in summary:
which is just what we wanted to show.
Edit: The discussion is also related to the relation of the length and velocity gauge for computing oscillator strengths. Some more information here.
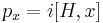
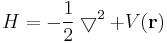
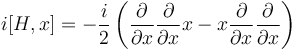
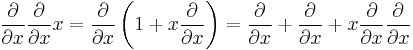

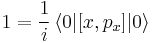


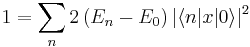

15 comments:
Hi Felix,
Random question. What is the physical significant of the transition dipole moment operator?
Hi, it is not so easy to put that into one sentence. But the idea is: If you look at the interactions of an oscillating electric field (i.e. light) with a molecule, you will find out that the transition dipole moment is the dominant quantity determining the strength of the interaction.
Hi Felix,
What about if two excited states are degenerated. In my opinion, we need to sum the transition dipoles moment associated with each excited states. Could you confirm it?
With best regards
Hi Felix,
You mention that the oscillator strength definition you gave is for non degenerate excited states. I guess that in case of degenerated excited states you have to sum up over transition dipole moments associated with each of the degenerated excited states in order to get the oscillator stregnth, right?
Many thanks in advance
Y
Hi, I am sorry I don't quite remember why I wrote this at the time. I guess the point I was making is: if the two states in the first formula are degenerate, then the oscillator strength equals zero. I don't know if that is a problem or not ...
-Felix
Hi Felix,
nice article!
Quick question, since I am newbie on the field: in the calculation of the Oscillator Strength in atomic units, the energy levels are in Hartree? The transition dipole moment is in Bohr?
Thanks,
T
Hi Felix,
nice article.
Quick question: the energy values to plug in the formula as it is define have to be in Hartree or eV? Which are the units, in this case, of the transition dipole moment?
Thanks
T
Hi, yes the easiest way to do it is to do everything in atomic units. This means that the energy levels are in Hartree and the transition dipole moments in unit-charge x Bohr.
-Felix
Thanks a lot for the answer!!!
Best,
T
sir can you explain how to intrepret the TDDFT TDA Excitation energies and how to find out lowest excited singlets and its near by triplets from that
Thanks Felix!
Is it meaningful then to have oscillator strengths f = 2? The common knowledge says it should 0 < f < 1 but from your discussion I don't see why it should be limited. Thanks in advance
Hi, oscillator strengths above 1 are no problem. This happens for example for conjugated polymers, see
Figure 1 of https://dx.doi.org/10.1021/jp400372t or
Table 1 of https://dx.doi.org/10.1039/C5CP07077E
Generally speaking, when you couple more and more chromophores within a Frenkel exciton model, the oscillator strength goes up to arbitrary large values.
-Felix
Thank you very much for your article!
Helped me a lot during writing my phd thesis :).
Hey Felix,
I do not understand where the 2 comes from at the last step of your calculation.
All those equations look a bit messed up, sorry ...
The idea is that each of the commutators is expanded as
[H,x] = Hx - xH
and then you let the H act on either the bra or the ket. In total you have four such terms, since you have two commutators. And at the end, there is a factor 2 left.
Post a Comment